MA.1
Zahl und Variable
B
Erforschen und Argumentieren
2
Die Schülerinnen und Schüler können Aussagen, Vermutungen und Ergebnisse zu Zahlen und Variablen erläutern, überprüfen, begründen.
Querverweise
MA.1.B.2
Die Schülerinnen und Schüler ...
1
a
- können Aussagen zu Anzahlen und Zahlpositionen an konkretem Material überprüfen (z.B. ein Turm mit 3 Klötzen ist höher als einer mit 2).
b
- können Summen und Differenzen mit Anschauungsmaterial überprüfen.
c
- können Produkte mit einer Summe überprüfen (z.B. 3 · 4 = 4 + 4 + 4).
- können Differenzen mit der Umkehroperation überprüfen (z.B. 27 - 6 = 21 → 21 + 6 = 27).
d
- können Quotienten mit der Umkehroperation überprüfen (z.B. 21 : 3 = 7 → 7 · 3 = 21).
2
e
- können Divisionen mit Rest mit der Umkehroperation begründen (z.B. 32 : 6 gibt Rest, weil 32 keine Zahl aus der 6er-Reihe ist).

f
- können Ergebnisse mit Überschlagsrechnungen überprüfen.
- können die Anzahl Stellen von Produkten und Quotienten erforschen und begründen.
g
- können Ergebnisse zu Grundoperationen durch Vereinfachen (z.B. 8 · 13 = 4 · 26 = 2 · 52), Zerlegen (z.B. 17.8 + 23.5 = 17 + 3 + 20 + 1.3) und Umkehroperationen überprüfen.
h
- können Aussagen zu arithmetischen Gesetzmässigkeiten erforschen, begründen oder widerlegen (z.B. eine ungerade Summe entsteht durch Addition einer geraden und einer ungeraden Zahl; die Produkte vier aufeinanderfolgender Zahlen sind durch 24 teilbar).
- können die Anzahl Nachkommastellen bei Produkten und Quotienten von Dezimalzahlen erforschen und begründen (z.B. mit Rechner).
3
i
- Erweiterung: können Äquivalenzumformungen mit Kontrollrechnungen überprüfen.

j
- können algebraische Aussagen durch Einsetzen von Zahlen überprüfen (z.B. a³ + 5a ist durch 6 teilbar: 4³ + 5⋅4 = 84 → 84 : 6 = 14;
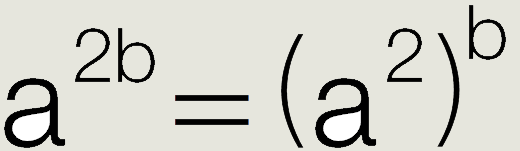 ; 2⁶ = (2²)³ = 2²˙³ = 4³; 2⁸ = 4⁴; 3⁴ = 9²).
; 2⁶ = (2²)³ = 2²˙³ = 4³; 2⁸ = 4⁴; 3⁴ = 9²).
k
- können Ergebnisse durch Verallgemeinern begründen (z.B. das Quadrat einer Zahl ist um 1 grösser als das Produkt der beiden Nachbarzahlen: 4 · 4 -1 = 3 · 5 → a² - 1 = (a - 1)(a + 1)).
- können Term- und Äquivalenzumformungen überprüfen.



